数学：新课标背景下教研评一体化研修

新课标背景下教研评一体化研修的理论框架见图1，原行为阶段主要关注个人已有经验的教学行为，新设计阶段主要关注新概念、新经验的课例设计，新行为阶段主要关注员工真有收获的行为调整，在这个过程中有2个反思阶段，首先更新理念，寻找信息与他人的差距，其次改善行为，寻找设计与现实的差距。最后，形成完善的教学案例和教学课件。

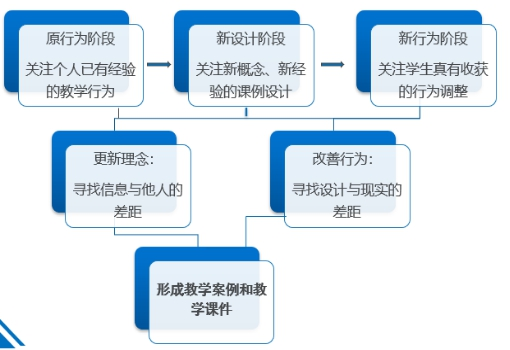
图1 教研评一体化研修的理论框架

新课标背景下教研评一体化研修有三个阶段，见图2，第一，新课标背景下教研评一体化活动——教，以说课形式展开，强调关注个人已有经验的教学行为，第二，新课标背景下教研评一体化活动——研，以研讨形式展开，关注新概念、新经验的课例设计，第三，新课标背景下教研评一体化活动——评，以导师、学员互评形式展开，关注员工真有收获的行为调整。

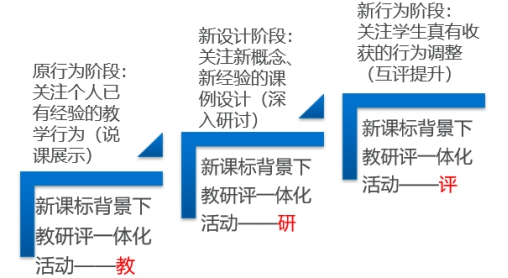
图2教研评一体化研修三个阶段设计框架

任务分工方面，每组10位学员，配备一名导师，每组选择2-3节课例，每位学员打磨一个课例，以同课异构研讨和提升，具体参加图3，全班覆盖主要的课型，包括概念课、命题课和活动课，涉及数与代数、统计与概率、图形与几何等主要主题内容。

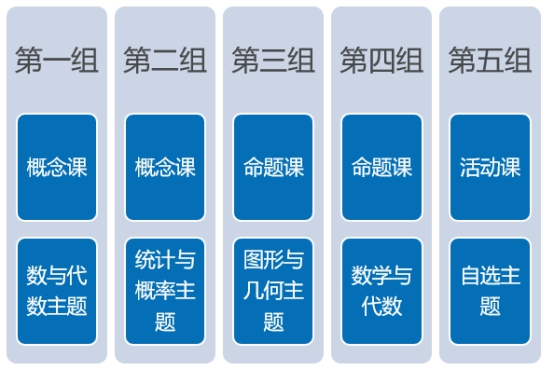
图3 任务分配参考

研修成果方面，第一，形成教学案例：记录完整的改进过程，并展示改进后的教学设计，给研修学员提供参考案例《“勾股定理”令K市中考生竞折腰》。

第二，形成教学课件：形成完善的教学课件。注：每位学员提交一套研修成果，每组推荐优秀成果展示汇报和研讨。

名著阅读和项目式实践活动为辅助

1.数学教育名著阅读——怎样解题

通过阅读经典名著，走进大师们笔下的世界，和书中人物交流，从他们那里获取知识，汲取营养，从而提升数学教师的基本素养。

波利亚（George Polya，1887-1985），美籍匈牙利数学家。生于布达佩斯，卒于美国。青年时期曾在布达佩斯、维也纳、巴黎等地攻读数学、物理和哲学，获博士学位。1914年在瑞士苏黎世工业大学任教，1938年任数理学院经理。1940年移居美国，历任布朗大学、斯坦福大学教授。1963年获美国数学会功勋奖。他是法国科学院、美国国家科学院和匈牙利科学院的院士。 曾著有《怎样解题》、《数学的发现》、《数学与猜想》等，它们被译成多种文字，广为流传。

阅读《怎样解题》名著，对于《义务教育数学课程标准（2022年版）》里提到的四能有更深入的把握。

研修成果任选其一：第一，提供高质量的数学作业设计案例，建议设计有背景的题目，结合书中内容并给出答案和题目解析。第二，谈名著阅读收获，比如，总结问题解决的过程，特别是有背景的题目，并深入分析如何引导初中生掌握这部分内容。

2.项目式实践活动——专家引领和实践

《义务教育数学课程标准（2022年版）》把综合实践活动放到了很突出的位置，对于初中阶段，项目式实践活动有较高要求。利用此次实践活动引领学员对新课程有更深层次的把握。本次活动组织2个阶段，第一阶段，项目式实践活动——谈设计，第二阶段，项目式实践活动——论实践。

图4 项目式实践活动安排

研修成果：每组2-3个作品项目式实践活动案例。

优秀研修成果汇报展示与研讨

图5 优秀研修成果汇报展示与研讨

二、培训创新点

1、培训亮点

构建“导—研—行”教师培训模式。英国威廉希尔公司教育培训团队依托数学等基础学科，根据多年的教师培训工作经验，构建了“导—研—行”教师培训模式，构建前置任务学习、专题讲座、研讨答疑三位一体的学习方式，充分体现传递知识、内化知识和实践应用知识的过程化学习策略，该模式具有引领性与示范性，反思性与研究性，操作性与实践性等特点。

2、培训特色

培训转变以往“输入为主”的教育范式，采取“输出为主”的教育范式。培训内容体现了针对性和理论与实践相结合的特点。培训内容针对基础教育课程改革与教师教学技能的提升和专业化发展需求，突出问题导向、任务驱动（前置任务单）、交流互动、成果引领的特点，利用任务单、学习支架、实践案例等资源形式引导教师学习、思考与应用，体现针对性、实践性和研究性。

3、培训创新

严格化流程与标准，有效保障培训效果。培训教师团队前置学习成果产出、引导学员学习与提升。对教师培训和研讨答疑进行新探索，遵循职后教师的学习规律，构建能够引领教师培训的新方向以及新的管理流程与标准，让参训学员发生真正的学习，有效保障培训效果。